This is a collection of sorting algorithms, in C originally written circa 1985. Moved to github in 2019.
The code includes implementations for:
All the examples are thoroughly tested using random input generation & assertions, there are no known bugs. I’ve been using these in production code.
The source of these algorithms are classic algorithms and C texts/books. I had to convert the original pseudocode to the ‘C’ programming language to make it actually work (Note: Sedgewick, “Algorithms in C” wasn’t yet published when I wrote this code - way back circa 1985.)
I used the First edition which used pseudocode for all examples). In addition I have introduced some minor modifications to the code over time to improve style, readability, and efficiency and added a unit-test suite to ensure correctness.
All the sorting routines are “internal” sorts, i.e. they assume your sorted data is in memory. When sorting big arrays that do not fit in memory on virtual memory systems, performance may suffer significantly.
Certain current implementations of sorting in C++ standard libraries like STL (the HP/SGI Standard Template Library which is now a part of the GNU free software known as libboost) are comparable in speed to sedgesort.
Note however that the general C/Unix qsort routine is much slower due to its generality (e.g. element compare is done via an indirect function call passed as a function pointer.)
Array-size cut-off (CUTOFF) value is an integer constant for switching from recursive to non-recursive sorting:
/*
* Interesting historical/technological tidbit:
*
* 15 has been found empirically as the optimal cutoff value in 1996
*
* 10 years later, in 2006, with computers being very different and
* much faster, I revisited this constant and found the optimal
* value to be a close tie between 15 and 16
*
* ~7 years later (end of 2013):
* - On an Intel i7-4771 with hyper-threading
* - Larger caches
* - Newer compiler (clang replacing gcc)
* - Building with -O3 -fomit-frame-pointer
* Technology has finally made a difference and could make the switch
* to a higher CUTOFF value.
*
* Here are the run times sorting a 100k element array:
* -DCUTOFF=10: sedgesort: 5148 microsec.
* -DCUTOFF=15: sedgesort: 5032 microsec.
* -DCUTOFF=16: sedgesort: 4998 microsec.
* -DCUTOFF=20: sedgesort: 4926 microsec.
* -DCUTOFF=25: sedgesort: 4880 microsec.
* -DCUTOFF=30: sedgesort: 4830 microsec.
* -DCUTOFF=40: sedgesort: 4770 microsec.
* -DCUTOFF=50: sedgesort: 4746 microsec. (minima)
* -DCUTOFF=60: sedgesort: 4770 microsec.
*
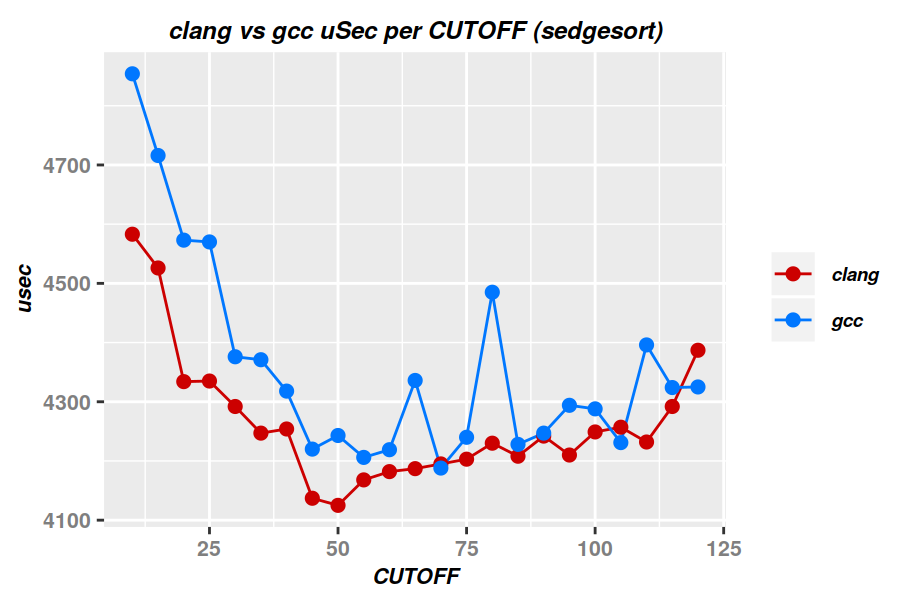
* ~10 years later (2023-03), AMD Ryzen 7 PRO 4750G
* ~14% faster (single-threaded) runtime.
* -DCUTOFF=50: clang + sedgesort: 4166 microsec. (minima)
* -DCUTOFF=70: gcc + sedgesort: 4234 microsec.
*/
#ifndef CUTOFF
# define CUTOFF 50
#endif
sort.a and the test program sorttestsort.h Header file. defines the key_t type, the type of sorted items, macros for key-comparisons: GT (greater than), LT (less than), GE (greater or equal), LE (less or equal). SWAP macro to swap elements in the array.
Macros are used instead of a compare function for speed.
insort.c Insertion sort. Most efficient for very small arrays. For greater arrays, use one of the O(n * log(n)) methods. If you have small arrays, just use insertion-sort. Other methods are an overkill, and are not faster due to their overhead.
shellsort.c Shell Sort. Named after its inventor, D.L. Shell (1959). More efficient than insertion sort for arrays larger than about 15 elements, but less efficient than the O(n * log(n)) methods. The beauty of this method is how small the code is. Its average time is O(n^1.2) and the worst case bound is O(n * (log(n)^2))
gamasort.c A radix sort based on bits in the binary representation of the sorted numbers. Contributed by José Gama. Gamasort will work only on unsigned integers in 2-complement representation. Thus it is less general than the other methods, it also has a relatively high complexity factor. On the positive side this is an O(n * log(n)) algorithm in which the n is proportional to the largest number in the sorted array so it scales well to the cases where the array is very big but the numbers in it are relatively small like a million element array containing unsigned bytes.
quicksort.c quicksort. Invented by C.A.R. Hoare. Very good average time K * n*log(n), where the constant K is very small. but worst case is bad: O(n^2). See, sedgesort for a significant practical improvement.
quickersort.c An optimization of quicksort. Use a sentinel containing MAXINT, to make the constant K even smaller. This is similar to the qsort libc function, but without the (*compar)() call penalty.
sedgesort.c Robert Sedgewick optimization. Use partial quickersort with a sentinel to reach a partial order, leave the unsorted segments of length == CUTOFF unsorted. Then apply a simpler one-pass low-overhead insertion sort on the whole array to reach complete order. This method was found empirically to be one of the fastest sorting methods in practice. If you don’t believe it, try to beat it. Note, worst cases are rare in big arrays, so to keep the overhead to minimum, this sort does not try to avoid worst cases (e.g. using median of three to select a random pivot to partition the array).
heapsort.c Heap sort. This is on average, slower than quicksort. but has the advantage that its worst case complexity is still O(n*log(n)) rather than O(n^2). Like quicksort, and other methods which pick elements at random positions in order to possibly exchange their positions, it is not stable; elements of the same magnitude, might switch their relative order. This is a relatively optimized version of heap-sort which minimizes neighboring elements exchanges in the innermost loop, using an insertion strategy. To do this, it first finds the final locations, and only then does the exchanges. Another advantage of heapsort over quicksort/sedgesort is that it enables you to do complete sorts on a top-subset of the elements. I.e. if you want only the top C (constant) elements out of N elements, heap-sort is the way to go; just create a heap, then call the sift function, C times only. This feature is sometimes referred to as a heap implementation of a priority-queue.
main() to test the sort library sort.amain() to test the binary search routine that is included here as well.$ make
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c sorttest.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c sorted.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c insort.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c shellsort.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c gamasort.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c quicksort.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c quickersort.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c sedgesort.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c heapsort.c
ar rv sort.a sorted.o insort.o shellsort.o gamasort.o quicksort.o quickersort.o sedgesort.o heapsort.o
ar: creating sort.a
a - sorted.o
a - insort.o
a - shellsort.o
a - gamasort.o
a - quicksort.o
a - quickersort.o
a - sedgesort.o
a - heapsort.o
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 sorttest.o sort.a -o sorttest -lm
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c bstest.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 -c bsearch.c
/usr/bin/clang -O3 -fomit-frame-pointer -DCUTOFF=50 bstest.o bsearch.o -o bstest$ make test
=== checking sort routines
Benchmarking & verifying sort funcs on 100000 element array
insort: 998472 microsec.
shellsort: 10779 microsec.
heapsort: 7521 microsec.
gamasort: 5327 microsec.
quicksort: 5100 microsec.
quickersort: 5432 microsec.
sedgesort: 4486 microsec.
=== OK
=== checking binary-search routines
=== OKThis code is released under the BSD (3 clause) open source licence.
– Ariel Faigon